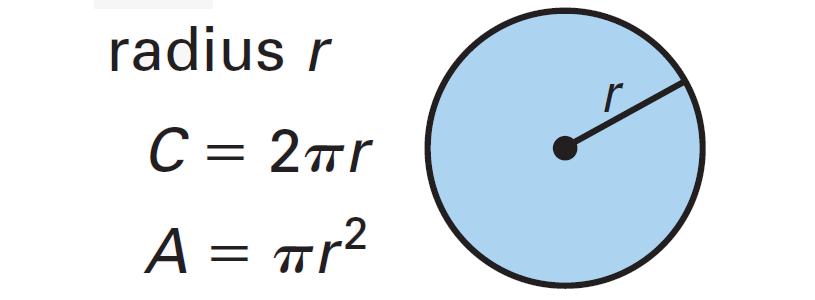If you have the area of a circle and want to find its circumference, you’re in the right place. Calculating the circumference of a circle using its area requires the use of a simple formula and some basic math. This article will guide you through the steps to find the circumference of a circle using its area, ensuring you have the necessary skills and knowledge to solve this problem.
Step 1: Start by identifying the area of the circle. You may have been given this information in a problem or you may need to measure it yourself using a formula or a measuring tool.
Step 2: Use the formula A = πr^2 to find the radius of the circle. In this formula, A represents the area of the circle and r represents the radius.
Step 3: Take the square root of the area divided by π to find the radius. This will give you the length of the radius in terms of the area.
Step 4: Once you have the value for the radius, double it to find the diameter. The diameter is the distance across the widest part of the circle, passing through the center.
Step 5: Use the formula C = πd to find the circumference, where C represents the circumference and d represents the diameter.
Step 6: Plug in the value for the diameter you calculated in step 4 into the formula C = πd, and solve for the circumference.
Step 7: Calculate the circumference using the formula C = 2πr. This formula uses the radius instead of the diameter.
Step 8: Compare the two values for the circumference calculated in steps 6 and 7. Ideally, they should be the same, but there may be slight variations due to rounding errors or approximations used in the calculations.
Step 9: Make any necessary adjustments or refinements to your calculations to ensure accuracy. This may involve double-checking your math, using more precise measurements, or seeking additional guidance or information.
Step 10: Write down your final answer and make sure to include the units of measurement, such as inches or centimeters, to provide context for your answer.
By following these steps, you can easily find the circumference of a circle using its area. This skill can be useful in a variety of practical and academic applications, from calculating the size of a circular object to solving math problems and equations. With practice, you will become more comfortable and proficient in using these formulas and calculations.
Understanding the Relationship Between the Area and Circumference of a Circle
The area and circumference of a circle are two fundamental measurements that are closely related. These measurements provide valuable information about the shape and size of a circle. Understanding the relationship between the area and circumference of a circle can help us solve various mathematical problems and practical applications.
The area of a circle is the measure of the region enclosed by its circumference. It can be calculated using the formula: A = πr^2, where A represents the area and r is the radius of the circle. The area is expressed in square units, such as square inches or square meters.
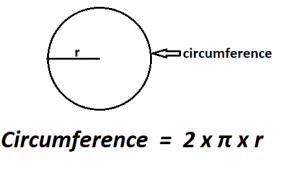
The circumference, on the other hand, is the distance around the outer boundary of the circle. It can be found using the formula: C = 2πr, where C represents the circumference and r is the radius of the circle. The circumference is expressed in linear units, such as inches or meters.
There is a direct relationship between the area and circumference of a circle. As the area increases, the circumference also increases. Similarly, as the circumference increases, the area also increases. This relationship is due to the fact that both measurements depend on the radius of the circle.
The radius is the distance from the center of the circle to any point on its boundary. Since the radius is a constant value for a given circle, any changes in the area or circumference must be proportional to the radius. Therefore, if we increase the radius, both the area and circumference will increase. Conversely, if we decrease the radius, both the area and circumference will decrease.
This relationship between the area and circumference of a circle is essential in various fields, such as geometry, physics, and engineering. It allows us to solve problems involving circles, such as finding the area of a circular garden or calculating the circumference of a circular race track. Understanding this relationship can greatly enhance our mathematical abilities and problem-solving skills.
Steps to Find the Circumference of a Circle Using Its Area
Calculating the circumference of a circle using its area is a straightforward task that can be done through a simple formula. By following a few steps, you can easily find the circumference of any circle using its area. Here is a summary of the steps:
- First, identify the given area of the circle. This could be provided in square units such as square centimeters or square inches.
- Next, apply the formula for finding the radius of a circle using its area. The formula is: radius = sqrt(area / pi), where sqrt denotes the square root and pi is a constant value approximately equal to 3.14159.
- Once you have the radius determined, calculate the circumference using the formula: circumference = 2 * pi * radius, where 2 represents twice the value and pi is the same constant as before.
- Plug in the value of the radius into the circumference formula and calculate the result.
- Round the final answer to the desired level of precision, depending on the given information or the requirements of the problem.
By following these steps, you can efficiently find the circumference of a circle using its area. Remember to always double-check your calculations and use the correct formula to ensure accurate results.