How to Convert Hexadecimal to Binary or Decimal – 6 Steps

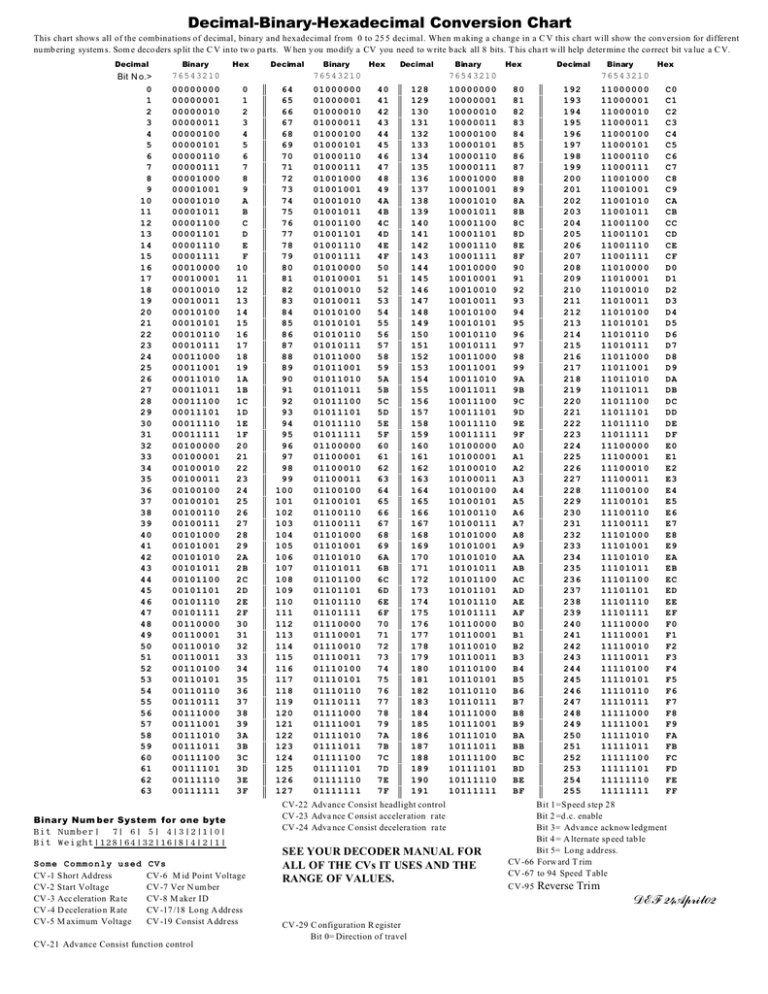
Converting hexadecimal numbers to binary or decimal is a crucial skill when working with computer systems and programming. Hexadecimal numbers are base-16 numbers that use the digits 0-9 and the letters A-F to represent values. While hexadecimal numbers may seem intimidating at first, converting them to binary or decimal is a straightforward process that can be done in just a few steps.

In this article, we will guide you through the process of converting hexadecimal numbers to binary or decimal using simple steps. Whether you are a beginner or already familiar with hexadecimal numbers, this guide will help you become more comfortable and confident when converting between different number systems.

To convert a hexadecimal number to binary, you need to break down the hexadecimal digits into their equivalent binary form. Each hexadecimal digit represents a group of four binary digits. By understanding this relationship, you can easily convert any hexadecimal number to binary by replacing each digit with its binary counterpart.

On the other hand, if you want to convert a hexadecimal number to decimal, you need to understand the place value system. Each digit in a hexadecimal number has a specific value based on its position. By multiplying each digit by its corresponding place value and adding them together, you can obtain the decimal equivalent of a hexadecimal number.

Converting Hexadecimal to Binary

Hexadecimal is a number system that uses base 16, with each digit representing a value from 0 to 15. This number system is commonly used in computer science and digital electronics. While hexadecimal is a convenient way to represent large binary numbers, it is often necessary to convert it to binary for various calculations or programming tasks.

To convert a hexadecimal number to binary, you can simply take each digit and replace it with its equivalent 4-bit binary representation. For example, the hexadecimal number “1A” can be converted to binary by replacing “1” with “0001” and “A” with “1010”, resulting in “00011010”.

To convert a longer hexadecimal number to binary, you can repeat this process for each digit. For instance, the hexadecimal number “32F” would be converted to “001100101111”. It is important to keep in mind that each digit of the hexadecimal number represents a multiple of powers of 16.

Another way to convert hexadecimal to binary is by using a hexadecimal to decimal conversion as an intermediate step. First, convert the hexadecimal number to decimal using the appropriate powers of 16. Then, convert the decimal number to binary using the standard process of dividing by 2 and noting the remainders.

Converting hexadecimal to binary is a fundamental skill in computer science and digital electronics. It allows for easier manipulation and calculation of binary numbers, which are the foundation of all digital systems. Whether you choose to use the direct substitution method or the hexadecimal to decimal conversion method, understanding this process will greatly enhance your understanding of number systems and their applications.

Step 1: Understand the hexadecimal system

The hexadecimal system is a positional numeral system that uses a base of 16. In contrast to the decimal system, which uses a base of 10, the hexadecimal system uses a combination of digits and letters to represent numbers.

In the hexadecimal system, the digits range from 0 to 9, and the letters A to F represent the values 10 to 15. This system is commonly used in computer programming and digital electronics because it allows for a more compact representation of binary data.

Each digit in a hexadecimal number represents a power of 16. The rightmost digit represents 16^0 (which is 1), the next digit to the left represents 16^1, the next digit represents 16^2, and so on.

To convert a hexadecimal number to binary or decimal, it’s important to have a good understanding of the hexadecimal system and how the digits and letters correspond to their respective values.

Step 2: Break down the hexadecimal number into individual digits

In order to convert a hexadecimal number to binary or decimal, it is necessary to break down the number into its individual digits. This step helps in identifying the value of each digit and simplifies the conversion process.

To break down a hexadecimal number, start from the rightmost digit and move towards the left. Each digit represents a power of 16, starting from 0 on the rightmost side. The value of each digit can be calculated by multiplying the digit with the corresponding power of 16.

• Example: Let’s break down the hexadecimal number “3A” into individual digits.

4-bit Group	Hexadecimal Digits	Decimal Values
Group 1	3	3 x 16^1 = 48
Group 2	A	10 x 16^0 = 10

In the example above, the hexadecimal digit ‘3’ represents the value 48 in decimal, and the digit ‘A’ represents the value 10 in decimal. Breaking down the hexadecimal number into individual digits allows for a clear understanding of the number’s composition and facilitates conversion to binary or decimal.

Step 3: Convert each digit to its binary equivalent

Now that we have a hexadecimal number, we can convert each digit to its binary equivalent. This step is quite simple and involves replacing each digit with its binary representation.

To do this, we can refer to a conversion table that lists the hexadecimal digits and their binary equivalents:

Hexadecimal Digit	Binary Equivalent
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

Using this table, we can convert each digit of the hexadecimal number to its binary equivalent. For example, if we have the hexadecimal number 3A, we would convert the digit ‘3’ to ‘0011’ and the digit ‘A’ to ‘1010’.

By converting each digit to its binary equivalent, we can now represent the original hexadecimal number in binary. This binary representation will be useful in further calculations or conversions, such as converting the hexadecimal number to decimal.